Conway’s Game of Life¶
Oppgave¶
Conway er kjent som oppfinner av spillet Game of Life (eller kort Life), som var en videreutvikling og forenkling av ideer fra John von Neumann. Spillet ble først publisert i 1970 i Scientific American innenfor Martin Gardners rubrik Mathematical Games. Spillet har det teoretiske potentiale av en Turing maskin, det vil si alt som kan beregnes algoritmisk kan også beregnes innenfor Game of Life. På grunn av Lifes analogier med vekst, nedgang og forandring tilhører den den økende klassen av såkalte simulation games. Spillet har fått avgjørende betydning for utviklingen av såkalte cellulære automater. (Fra SNL)
 Eksempel på Game Of Life
Eksempel på Game Of Life
Spillet går ut på at det er et eneste stort rutenett. Rutene kan være enten opplyste (levende) eller tomme (døde).
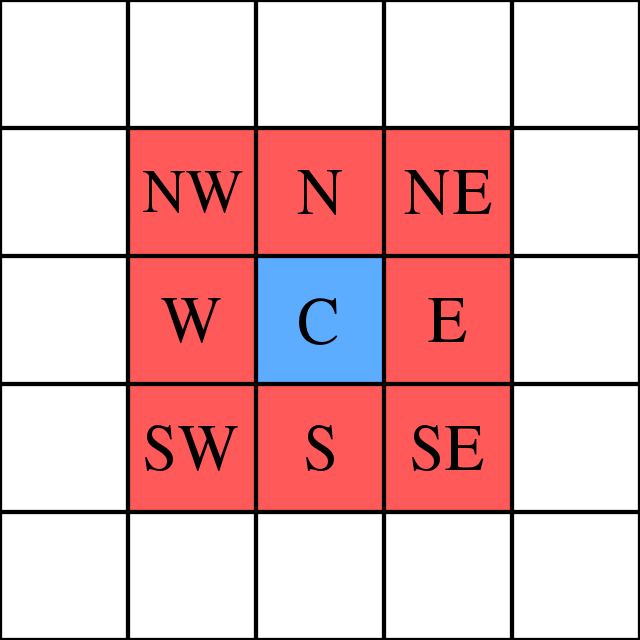 Alle celler spillet har ni naboceller.
Alle celler spillet har ni naboceller.
Spillet er bygget på følgende regler:
1. En levende celle med færre en to levende naboer dør av ensomhet.
2. En levende celle med to eller tre levende naboer overlever til neste generasjon.
3. En levende celle med fler enn tre naboer dør på grunn av overbefolkning.
4. En død celle med nøyaktig tre naboer blir levende som ved reproduksjon.
Oppgave: Lag Game of Life!
Denne oppgaven kan være godt egnet for å løses sammen med andre.¶
Denne oppgaven er laget av fuzzbin og bitjungle. Oppgaven er lisensiert under en Creative Commons Navngivelse-DelPåSammeVilkår 4.0 Internasjonal lisens.